2013.05.07
カテゴリ:作品
今日の文章題 「色紙」
最近3週間ほど取り組んでいた問題があり昨日ついに解ききった。
問題
A、B、Cの3人が始めにそれぞれ何枚かの色紙を持っていて、AとCの差は9枚でした。AがBにAがはじめに持っていた色紙の1/3をあげ、次にBがAから色紙ももらった後にその時Bが持っていた色紙の2/5をCにあげ、最後にCはBから色紙をもらった後にその時Cが持っていた色紙の1/3をAにあげたところ、A、B、Cが持っている色紙の枚数の比は、10:9:8になりました。はじめにAが持っていた色紙は何枚ですか。
- なかなかの難問である。数学を使えばこんなものは秒殺できるがそんな低レベルなものを私達は目指してなどいない。
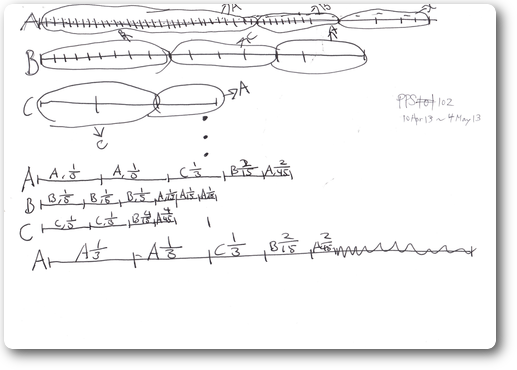
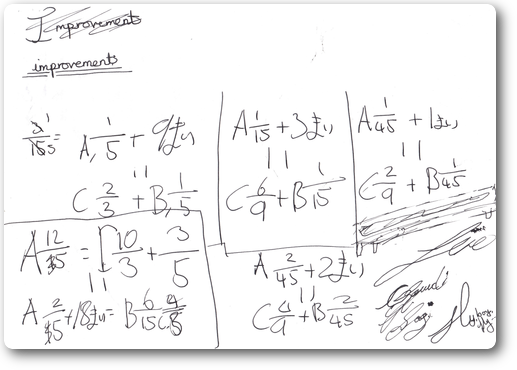
- すべてオリジナルのイメージ図を駆使して解くのである。3変数の連立方程式でやれば簡単な問題だがそんなことは誰でもできるし、そもそもそんなやり方しか知らずに解いたって1+1を解くことと大差はない。
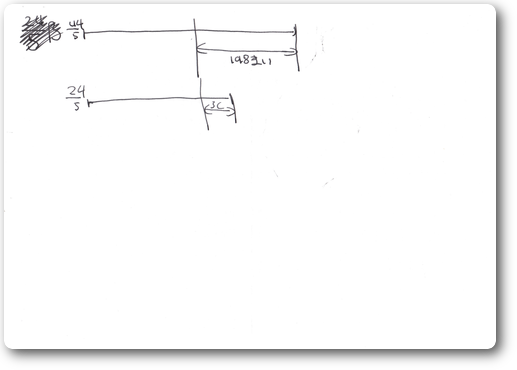
- 子供は膨大(30枚以上は軽く使った)な紙面を割いてイメージ図から3本の関係を抽出し、そこから果てしなくイメージを動かして目的に到達した。
- そのなかで特筆すべきことはAとCの差が9枚という条件で、C+9=Aとした点だ。私は偶然Aの方がCより大きいと思い込んでたまたま導けたと思ったが違うのである。
- 子供は常にA+9=CかC+9=Aを考えており、繰り返しイメージする中でC+9=Aでなければmake senseではないと確信して導いていた。このセンスには脱帽だ。
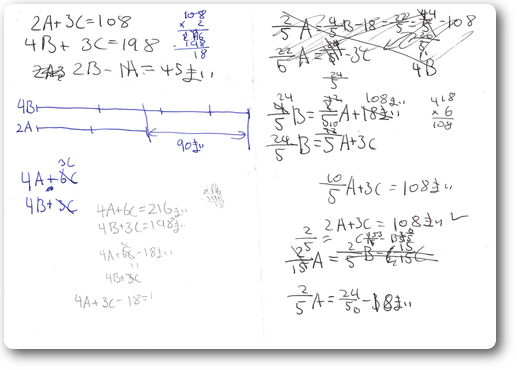
- 今回の問題で初めて自分からオリジナルの数式を使い始めた。いままで一度も教えたこともないし学校でもほんの少しやっただけのようだ。
- 最初から数式を使ってはいなかったが繰り返し図を書く中で自然に自分の分かりやすい書き方で数式を使い始めたのである。明確なステージアップであると感じた。
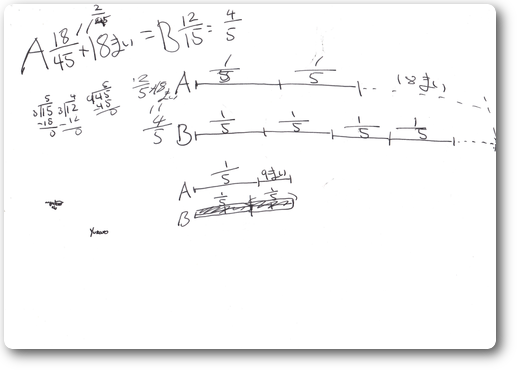
- かなり複雑な分数の式となるがそれを最も簡潔な3本の式にして抽出していることは驚きだった。分数自体計算の訓練は避けているので全くやっておらず毎回分数の意味を考えながらカタツムリのスピードでやっている。
- 今回の問題で分数と数式の扱いもオリジナルの工夫によって相当上達したようだ。
- 解けない問題に対する姿勢がすばらしいことも特筆すべきことのひとつ。実にマイペースで日々時間のあるときを見つけて考え続けていた。学校にも紙切れをポケットに忍ばせ時間があるときに考えていたそうである。この姿勢はすでに研究者の姿勢と同じだ。昔私が大学院で数学者を目指していたときの姿に重なる。なんとも親ばかであるが頼もしい限りである。
- 蛇足であるがこんなことができるセンスを持っている子をSelective Schoolは見つけることができないのである。先取りした知識を使い単純な問題を猛烈なスピードで解く訓練をした子供を選んでいる。英国にも日本にも思考力とは何かという根本的なノウハウは存在していない。