2014.07.26
カテゴリ:作品
今日の文章題 「4目ならべ」
今回は2002年ジュニア・算数・広中杯ファイナルNo4を選びました。
- ピータと平ちゃんがちょっと変わった「4目ならべ」で遊んでいます。たて6列、横6列の計36個もマスの中に、ピーターが黒石を、平ちゃんが白石を置きます。
ピーターが最初にいくつかの黒石を置き、次に平ちゃんが空いているマスの中にすきなだけ白石を置きます。ピーターの目的は、平ちゃんがどれだけ白石を置いても、平ちゃんに「4目」をつくらせないこと、つまり4つの白石が1列(たて・横・ななめ)にならばせないようにすることです。- (1) ピーターは最少で何個の黒石を置けばいいですか。
- (2) (1)の置き方のうち、ピーターの置いた黒石が「4目」を作っているような置き方を考えられるだけ答えなさい。ただし、答えの図のうち回転させたり、裏返したりして、すべての黒石の位置が重なるものは同じ答えとみなします。
今回の問題は相当やっかいな問題でしたが解けました。子供の好きなタイプの問題だったようでとても楽しんでいました。Try&Errorでひたすらやるのではなくある程度理論的に導いていることには驚きました。
考え方
- 6つの黒石を一列に並べる。2枚目の一番最初の図。
- こうすることで「たて」と「ななめ」は全部おさえることができる。
- そのうちのいくつかを前に出すことを考える。
- できるだけ効率よく「隙」を消すため。
- 2マス前に進めてしてしまうと失敗するので1マスだけ前にだす。
- マスの取り方によってできる「隙」のタイプを見ていくことで分かる。
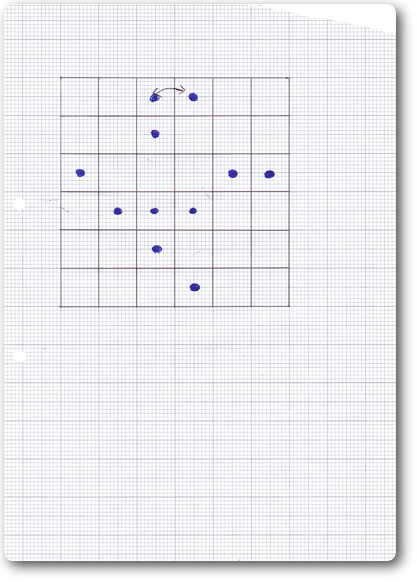
- 前に出す黒石の数は3つが最適であることを特定する。Tickのしてある図。
- 進める黒石の個数によってできる「隙」のタイプを見ていくことで分かる。
- ここまでくればあとは簡単にできる。
- 答え:黒石は10個必要で、3枚目の図で矢印のついている黒石はどちらでも良いので2種類ある。
子供は2枚目のTickが付いている置き方が最も良いと直感したとのこと。子供はチェスが大好きですが、この陣形が一番強いと考え試してみたそうです。
この発想のレベルまでくるともう私の力ではついていけないです。ちなみに模範解答とはまるで違う方法です。子供の考え方の方がはるかに芸術的だと感じます。どんぐり理論でいう小脳思考なのかもしれません。